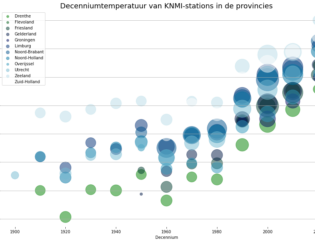
Linear regression is het meestgebruikte algoritme in machine learning modellen. In een lineair regression model kun je verbanden ontdekken tussen de door de data scientist gekozen features en de zogenaamde doel-column. Met linear regression voorspel je altijd numerieke waarden. Bijvoorbeeld iemands BMI o.b.v. levensstijl, of de huizenprijs o.b.v. kenmerken van het huis en de buurt.
Op deze pagina vind je uitleg over simple linear regression en multiple linear regression. Vervolgens geven we een voorbeeld van een regressiemodel waarmee de levensverwachting voor landen voorspeld kan worden op basis van diverse factoren. Je kunt dit zelf mee doen als een tutorial.
Inhoud pagina:
- Wat is linear regression?
- Wat is multiple linear regression?
- Een voorbeeld en tutorial van multiple linear regression in Python met package scikit-learn
Wat is linear regression?
Simple linear regression kent de volgende formule: y = ax + b.
Het is mogelijk om doelwaarde 'y' te bepalen op basis van inputwaarde 'x'. 'a' en 'b' zijn parameters die door het regressiemodel worden ingevuld zodat het model optimaal voorspelt. Als data scientist is het jouw taak om de inputwaarden (de feature column) slim te kiezen, zodat de voorspellende waarde van het model maximaal is.
Voor linear regression is het belangrijk om een aantal "assumptions" oftewel "aannames" te checken voordat je de resultaten uit jouw analyse gaat gebruiken. In dit artikel gaan we niet uitgebreid in op de assumpties die onder lineaire regressie liggen, maar in 7 assumptions bij linear regression kun je er alles over lezen.
Op deze pagina zullen we gebruik maken van deze dataset waarin de levensverwachting van inwoners van verschillende landen is opgenomen. Daarnaast bevat de dataset informatie over bijvoorbeeld alcoholgebruik, de voorkomendheid van verschillende ziekten, het GDP (Bruto nationaal product), geschooldheid van de populatie.
Om te laten zien wat simple linear regression is makken we in Python een scatterplot tussen de voorkomendheid van AIDS (x-as) en de levensverwachting van de bevolking (y-as). Je kunt je voorstellen dat hoe meer AIDS er voorkomt in een land, hoe korter de levensverwachting is van mensen in dat land.
plt.scatter(df_zonder_missing[' HIV/AIDS'], df_zonder_missing['Life expectancy '])
m, b = np.polyfit(df_zonder_missing[' HIV/AIDS'], df_zonder_missing['Life expectancy '], 1)
plt.plot(df_zonder_missing[' HIV/AIDS'], m*df_zonder_missing[' HIV/AIDS'] + b, c='g')
plt.xlabel('Voorkomendheid HIV/AIDS')
plt.ylabel('Levensverwachting in jaren')
plt.show()
Het is nu niet van belang om het Python script te begrijpen. Maar de groene lijn geeft de lijn weer die je met een simple linear regression model kunt achterhalen. In dit geval ziet de regressieformule er als volgt uit: levensverwachting in jaren = -0,86 * voorkomendheid HIV/AIDS + 71,02. Je kunt nu voor nieuwe datapunten een voorspelling doen.
Zoals in de grafiek te zien is bestaat er een duidelijke correlatie tussen de voorkomendheid van HIV/AIDS en de levensverwachting, maar laat de 'fit' van dit regressiemodel wel wat te wensen over. Later in de tutorial gaan we dieper in op hoe je kunt checken hoe jouw linear regression model presteert.
De lijn van een simple linear regression model wordt bepaald door voor alle datapunten te kijken welke lijn een minimale afstand geeft tussen de voorspelde waarde en de werkelijke waarde. Onderstaande 'error' wordt dus voor ieder punt berekend.
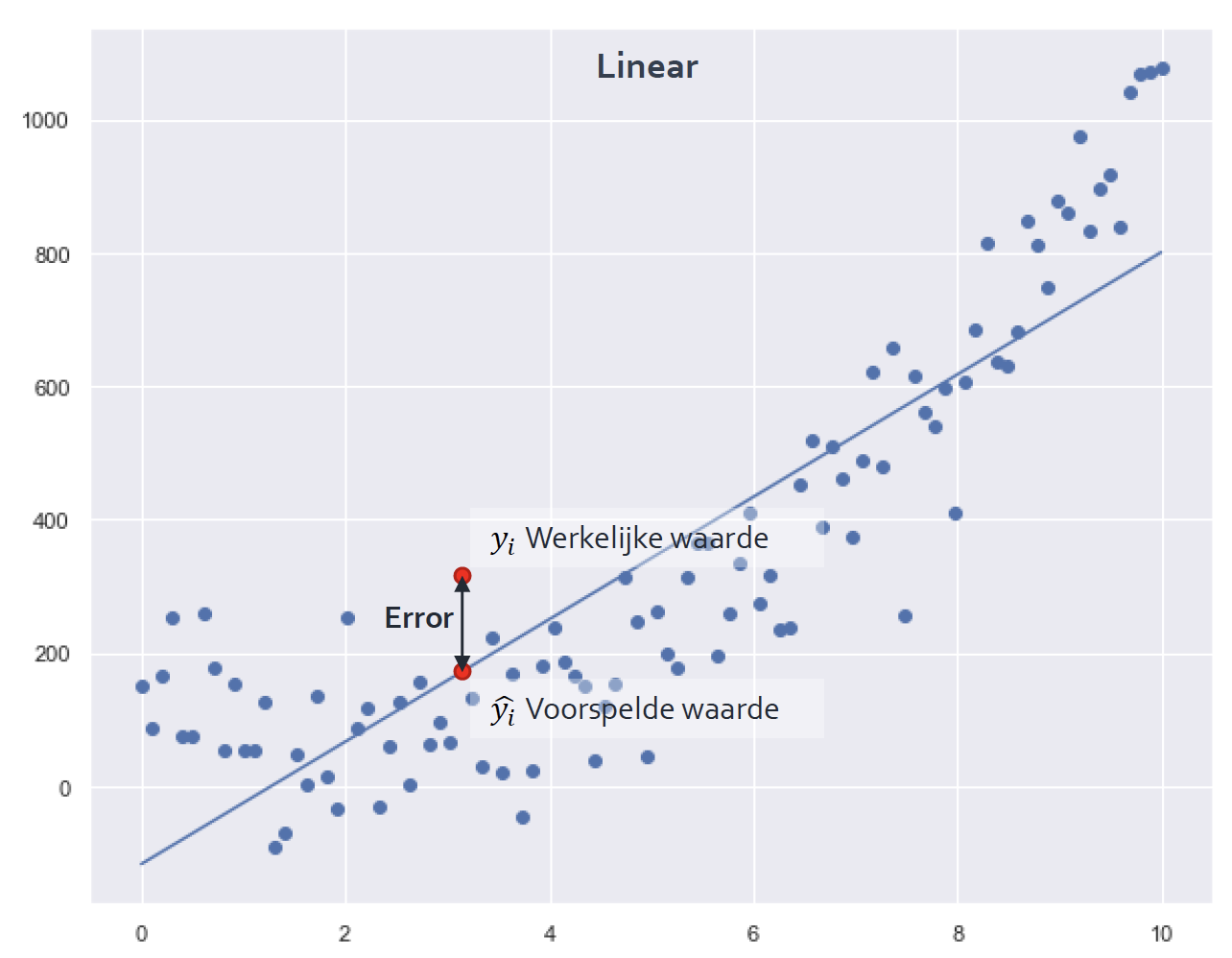
Dit wordt met de volgende formule gedaan:
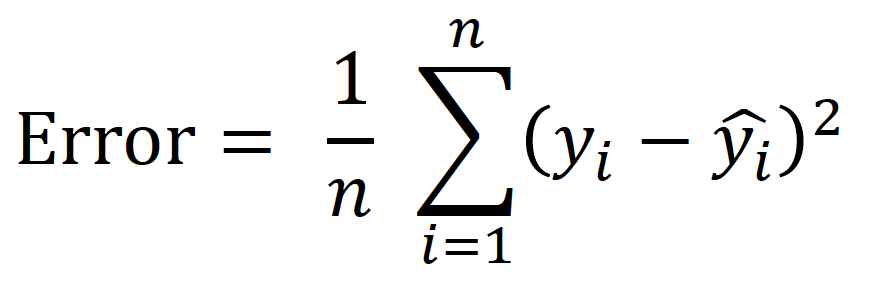
De 'error' wordt gekwadrateerd zodat we alleen positieve waarden overhouden. Alle waarden worden opgeteld en door het aantal datapunten gedeeld. Zo houd je de 'gemiddelde error' over, ook wel de Mean Squared Error (MSE) genoemd. De MSE waarde is een belangrijke indicator voor de voorspellende kracht van een machine learning model.
Wat is multiple linear regression?
Multiple linear regression (ook wel multiple regression genoemd) stelt ons in staat meerdere features (verschillende columns uit de dataset) te gebruiken als input om een doel-column (target) te voorspellen. De formule is vergelijkbaar met die van simple linear regression, uitgebreid met het aantal features dat je voor de voorspelling gebruikt:
y = a1x1 + a2x2 + ... + anxn + b
In een data science vraagstuk waarin multiple linear regression een rol speelt is feature selectie uitermate belangrijk. Oftewel; welke columns uit de dataset hebben de grootste voorspellende waarde voor de target variabele. Identificeren welke features belangrijk zijn kan op basis van literatuuronderzoek, expert-interview, of bijvoorbeeld door te kijken naar welke features een hoge correlatie hebben met de target column. Ook heb je minder aan feature columns waarin de variantie laag is. Hoe verschillender de waarden in een column, hoe potentieel waardevoller in een voorspelmodel.
Het is lastig om je van een multiple linear regression model een visuele voorstelling te maken omdat het het twee- of driedimensionale overstijgt. Om meer gevoel bij de kracht van multiple regression te krijgen zullen we een voorbeeld in Python uitwerken waarbij het package scikit-learn wordt gebruikt.
Een voorbeeld en tutorial van multiple linear regression in Python met package scikit-learn
We zullen nu in een tutorial multiple linear regression toepassen in Python. We werken met de eerder geïntroduceerde dataset.
Als je mee wilt doen:
- Installeer je Python (als je dat nog niet hebt gedaan)
- Installeer je Jupyter Notebook (als je dat nog niet hebt gedaan)
- Installeer je de benodigde packages (als je dat nog niet hebt gedaan)
Allereerst zullen we de benodigde packages importeren en de dataset inlezen. Let op dat je de benodigde packages hebt geïnstalleerd op je computer.
import numpy as np
import pandas as pd
import math
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
df =pd.read_csv('Life Expectancy Data.csv')
print(df.info())
df.head()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2938 entries, 0 to 2937
Data columns (total 22 columns):
Country 2938 non-null object
Year 2938 non-null int64
Status 2938 non-null object
Life expectancy 2928 non-null float64
Adult Mortality 2928 non-null float64
infant deaths 2938 non-null int64
Alcohol 2744 non-null float64
percentage expenditure 2938 non-null float64
Hepatitis B 2385 non-null float64
Measles 2938 non-null int64
BMI 2904 non-null float64
under-five deaths 2938 non-null int64
Polio 2919 non-null float64
Total expenditure 2712 non-null float64
Diphtheria 2919 non-null float64
HIV/AIDS 2938 non-null float64
GDP 2490 non-null float64
Population 2286 non-null float64
thinness 1-19 years 2904 non-null float64
thinness 5-9 years 2904 non-null float64
Income composition of resources 2771 non-null float64
Schooling 2775 non-null float64
dtypes: float64(16), int64(4), object(2)
memory usage: 505.0+ KB
None
| Country | Year | Status | Life expectancy | Adult Mortality | infant deaths | Alcohol | percentage expenditure | Hepatitis B | Measles | ... | Polio | Total expenditure | Diphtheria | HIV/AIDS | GDP | Population | thinness 1-19 years | thinness 5-9 years | Income composition of resources | Schooling | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Afghanistan | 2015 | Developing | 65.0 | 263.0 | 62 | 0.01 | 71.279624 | 65.0 | 1154 | ... | 6.0 | 8.16 | 65.0 | 0.1 | 584.259210 | 33736494.0 | 17.2 | 17.3 | 0.479 | 10.1 |
| 1 | Afghanistan | 2014 | Developing | 59.9 | 271.0 | 64 | 0.01 | 73.523582 | 62.0 | 492 | ... | 58.0 | 8.18 | 62.0 | 0.1 | 612.696514 | 327582.0 | 17.5 | 17.5 | 0.476 | 10.0 |
| 2 | Afghanistan | 2013 | Developing | 59.9 | 268.0 | 66 | 0.01 | 73.219243 | 64.0 | 430 | ... | 62.0 | 8.13 | 64.0 | 0.1 | 631.744976 | 31731688.0 | 17.7 | 17.7 | 0.470 | 9.9 |
| 3 | Afghanistan | 2012 | Developing | 59.5 | 272.0 | 69 | 0.01 | 78.184215 | 67.0 | 2787 | ... | 67.0 | 8.52 | 67.0 | 0.1 | 669.959000 | 3696958.0 | 17.9 | 18.0 | 0.463 | 9.8 |
| 4 | Afghanistan | 2011 | Developing | 59.2 | 275.0 | 71 | 0.01 | 7.097109 | 68.0 | 3013 | ... | 68.0 | 7.87 | 68.0 | 0.1 | 63.537231 | 2978599.0 | 18.2 | 18.2 | 0.454 | 9.5 |
5 rows × 22 columns
Om linear regression toe te kunnen passen is het van belang dat er geen missing values in de dataset zitten. We zien dat diverse columns missende waarden bevatten. Je kunt deze missende waarden opvullen met bijvoorbeeld het gemiddelde, de mediaan, of de modus van een column. Of je kunt op basis van een hoog-correlerende variabele de missende waarden opvullen. Je kunt ook besluiten een column buiten beschouwing te laten, bijvoorbeeld wanneer er een andere column zeer sterk correleert en het dus eigenlijk bijna een dubbeling is.
Wij kiezen er hier voor om alle rijen met missende waarden te verwijderen. Dat is niet heel netjes, maar het behandelen van missing values is niet het onderwerp van deze pagina. Bovendien houden we nog ruim voldoende complete datapunten over.
df.isnull().sum()
Country 0
Year 0
Status 0
Life expectancy 10
Adult Mortality 10
infant deaths 0
Alcohol 194
percentage expenditure 0
Hepatitis B 553
Measles 0
BMI 34
under-five deaths 0
Polio 19
Total expenditure 226
Diphtheria 19
HIV/AIDS 0
GDP 448
Population 652
thinness 1-19 years 34
thinness 5-9 years 34
Income composition of resources 167
Schooling 163
dtype: int64
df_zonder_missing = df.dropna()
print(df_zonder_missing.isnull().sum())
print(df_zonder_missing.shape)
Country 0
Year 0
Status 0
Life expectancy 0
Adult Mortality 0
infant deaths 0
Alcohol 0
percentage expenditure 0
Hepatitis B 0
Measles 0
BMI 0
under-five deaths 0
Polio 0
Total expenditure 0
Diphtheria 0
HIV/AIDS 0
GDP 0
Population 0
thinness 1-19 years 0
thinness 5-9 years 0
Income composition of resources 0
Schooling 0
dtype: int64
(1649, 22)
Wanneer je bezig gaat met feature selection of met de zojuist besproken missing values, dan kan een heatmap van correlaties helpen. De toepassingen voor missing values zijn net besproken. Voor feature selection kun je een heatmap gebruiken door:
- Features te selecteren met een sterke (positieve of negatieve) correlatie met de target variabele
- Features die sterk met elkaar correleren niet dubbel te selecteren omdat ze wellicht dezelfde informatie in zich hebben (denk bijvoorbeeld aan aantal kamers in een huis en aantal vierkante meters in een huis. Dit zijn andere features maar hebben ruwweg hetzelfde voorspellend vermogen)
Een heatmap van correlaties genereer je makkelijk in Python. Dit doe je als volgt.
correlaties = df_zonder_missing.corr()
sns.heatmap(correlaties)
<matplotlib.axes._subplots.AxesSubplot at 0x12009e0f0>
Onze informatie over onze dataset ziet er nu als volgt uit:
df_zonder_missing.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 1649 entries, 0 to 2937
Data columns (total 22 columns):
Country 1649 non-null object
Year 1649 non-null int64
Status 1649 non-null object
Life expectancy 1649 non-null float64
Adult Mortality 1649 non-null float64
infant deaths 1649 non-null int64
Alcohol 1649 non-null float64
percentage expenditure 1649 non-null float64
Hepatitis B 1649 non-null float64
Measles 1649 non-null int64
BMI 1649 non-null float64
under-five deaths 1649 non-null int64
Polio 1649 non-null float64
Total expenditure 1649 non-null float64
Diphtheria 1649 non-null float64
HIV/AIDS 1649 non-null float64
GDP 1649 non-null float64
Population 1649 non-null float64
thinness 1-19 years 1649 non-null float64
thinness 5-9 years 1649 non-null float64
Income composition of resources 1649 non-null float64
Schooling 1649 non-null float64
dtypes: float64(16), int64(4), object(2)
memory usage: 296.3+ KB
De columns 'Country' en 'Status' zijn categorische variabelen. Deze kun je niet zomaar gebruiken in een lineair regressiemodel, omdat een dergelijk model numerieke inputwaarden verwacht. Het is daarom noodzakelijk om hier dummievariabelen van te maken. Dit doen we als volgt.
land_dummy = pd.get_dummies(df_zonder_missing['Country'])
land_dummy.head()
| Afghanistan | Albania | Algeria | Angola | Argentina | Armenia | Australia | Austria | Azerbaijan | Bangladesh | ... | Tunisia | Turkey | Turkmenistan | Uganda | Ukraine | Uruguay | Uzbekistan | Vanuatu | Zambia | Zimbabwe | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
5 rows × 133 columns
status_dummy = pd.get_dummies(df_zonder_missing['Status'])
status_dummy.head()
| Developed | Developing | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 0 | 1 |
| 4 | 0 | 1 |
We verwijderen nu de oorspronkelijke 'country' en 'status' columns en voegen de dummyvariabelen toe aan de dataset. Zo eindigen we met een dataset zonder missing values en alleen numerieke inputwaarden. We splitsen de onze dataset op in inputvariabelen en onze target column. We gebruiken voor het gemak alle columns uit de dataset (behalve natuurlijk life expectancy) als voorspellers.
df_zonder_missing_dummy = df_zonder_missing.drop(['Country', 'Status'], axis = 1)
df_voor_ml = pd.concat([df_zonder_missing_dummy, land_dummy, status_dummy], axis = 1)
y = df_voor_ml['Life expectancy ']
X = df_voor_ml.drop('Life expectancy ', axis = 1)
Als je een machine learning model ontwikkelt dan splits je vaak je dataset op in 'traindata' en 'testdata'. Je wilt namelijk een model trainen met historische data, en vervolgens valideren met testdata die je nog niet hebt gebruikt. Het packages scikit-learn biedt standaard dergelijke functionaliteit.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)
We kunnen nu ons Linear Regression model gaan trainen. Dit doen we wederom met het package scikit-learn met het model LinearRegression(). Je kunt een model trainen met .fit() en je kunt voorspellingen maken met .predict().
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train, y_train)
predictions = lr.predict(X_test)
predictions[:10]
array([79.59181916, 71.28915252, 72.062185 , 73.28586538, 72.24028192,
68.1611105 , 66.43659447, 66.05456397, 67.31252755, 62.86038915])
Met bovenstaande code hebben we het model getraind met 'traindata'. Vervolgens hebben we het getrainde model een voorspelling laten doen op de testdata zodat we de prestaties van het model op onbekende data kunnen beoordelen. We kunnen nu de Mean Squared Error (eerder behanded op deze pagina) en de R2 berekenen. De R2 is de spreiding in de data die door het model verklaard wordt. Als dit 1 is voorspelt het model perfect.
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print(mean_squared_error(y_test,predictions)**(1/2))
print(r2_score(y_test,predictions))
1.6557070818049116
0.9641867228528007
We zien dat er een kleine MSE is en een hoge R2. Het model presteert dus goed.
Een Linear Regression model stap voor stap toepassen met Python is onderdeel van onze machine learning training en data science opleiding. Dus wil jij je ontwikkelen of omscholen tot data scientist en in staat zijn om nog nauwkeurigere voorspellingen te kunnen doen? Schrijf je dan in of neem contact met ons op voor meer informatie.
Download één van onze opleidingsbrochures voor meer informatie

Rik is data scientist en marketeer bij Data Science Partners. Vanuit zijn achtergrond op de Technische Universiteit Eindhoven heeft hij veel affiniteit met data. Na zijn studie heeft hij als consultant altijd met data gewerkt en tevens ervaring opgedaan in het geven van trainingen.