Met het Support Vector Machine (SVM) algoritme doet een data scientist voorspellingen door data in groepen te verdelen. Er is altijd een omschrijvende dataset nodig, hierdoor valt het SVM algoritme binnen Supervised Learning. Je kunt SVM gebruiken om zowel numerieke waarden te voorspellen (regressie) als om een groep of label te bepalen (classificatie). In de praktijk wordt het het meest gebruikt bij classificatie-vraagstukken.
Met het Support Vector Machine (SVM) algoritme kun je voorspellingen doen door data in groepen te verdelen
Uitleg Support Vector Machine
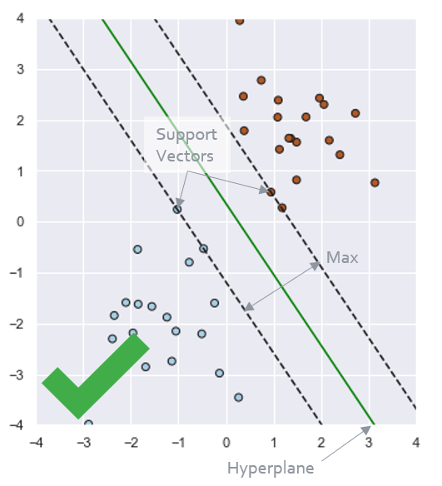
SVM verdeelt data in groepen met zogeheten hyperplanes door gebruik te maken van support vectors. Support vectors zijn de datapunten van verschillende groepen waar als je hier parallelle lijnen door zou trekken, de onderlinge afstand tussen deze lijnen (in geval van 2 dimensies) het grootst is. Het hyperplane is de lijn of het vlak wat hier tussenin ligt, en wat dus werkelijk de scheidingslijn is van de verschillende groepen.
Stel je dit als volgt voor. Je hebt een dataset met 2 eigenschappen (features) en 1 kolom die een groep aangeeft met 2 mogelijke waarden. Je kunt de datapunten tegen elkaar plotten, hierbij zet je de waarden van het ene feature op de x-as en van de andere feature op de y-as. Als je nu een lijn kan plotten die de datapunten van de 2 groepen kan scheiden, je de raaklijnen door de support vectors zo plaatst dat de onderlinge afstand maximaal is, dan ligt hiertussen het hyperplan. Datapunten die aan de ene kant van dit hyperplane vallen horen bij de ene groep, en datapunten die aan de andere kant van het hyperplane vallen horen bij de andere groep.
In de praktijk is dit lastig, er is niet altijd een mooie lijn te vinden die de groepen perfect scheidt. Stel dat de datapunten in ons voorbeeld met de 2 features elkaar deels zouden doorkruisen, waar hadden we dan de scheidingslijn getrokken? Dit is te verbeteren met wat Kerneling heet. Hierbij voeg je meer dimensies (extra features) toe waardoor de datapunten beter te scheiden zijn. In ons voorbeeld werkten we met 2 features, dit is 2-dimensionaal en hier kunnen we een scheidingslijn doorheen trekken. Wanneer we hier een derde feature aan toe zouden voegen wordt het een 3-dimensionaal geheel, en is er een vlak in plaats van een lijn nodig om de groepen te scheiden.
Wanneer gebruik je Support Vector Machine?
SVM is minder geschikt voor datasets met veel ruis, omdat ruis ervoor kan zorgen dat datapunten van verschillende groepen elkaar overlappen en doorkruisen. Daarnaast is het ook minder geschikt voor grotere datasets omdat de trainingstijd dan erg lang kan zijn. Je gebruikt SVM typisch bij kleinere datasets die behoorlijk 'schoon' zijn, hierbij zullen nauwkeurige voorspellingen gedaan kunnen worden.
Support Vector Machine met Python
In dit voorbeeld gaan we stap voor stap het SVM algoritme toepassen om een machine learning model te trainen voor een classificatievraagstuk. Dit doen we met een script in de programmeertaal Python. Omdat veel machine learning toepassingen in Python worden ontwikkeld is Python leren een waardevolle investering.
We werken hier met een iris dataset, een dataset met meetgegevens van bloemen en de toewijzing welke soort iris het betreft. Dit kan een van de volgende soorten zijn: setosa, virginica of versicolor. Hierbij behandelen we de volgende stappen:
- Onderzoeksvraag
- Data verzamelen
- Data voorbewerken
- Algoritme kiezen
- Model trainen
- Model beoordelen
1. Onderzoeksvraag
Wanneer we een verzameling meetgegevens van irisbloemen hebben, willen we kunnen voorspellen welk type iris (setosa, virginica of versicolor) van toepassing is op een meting.
2. Data verzamelen
De iris dataset is te importeren vanuit package Scikit-Learn. We doen dit als volgt:
from sklearn import datasets
iris = datasets.load_iris()
In deze dataset zijn de volgende eigenschappen (features) beschikbaar:
iris.feature_names
['sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)']
Het irissoort (setosa, virginica of versicolor) is al beschikbaar als numerieke waarde.
iris.target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
iris.target_names
array(['setosa', 'versicolor', 'virginica'], dtype='<U10')
We kunnen nu alvast een grafiek maken van deze data.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(color_codes=True)
X = iris.data[:, 2:]
y = iris.target
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(1,1,1)
for index, target_name in enumerate(iris.target_names):
ax.scatter(X[y == index, 0], X[y == index, 1], s=40, alpha=0.9, edgecolors='k', label=target_name)
ax.set_xlabel('petal_length')
ax.set_ylabel('petal_width')
ax.legend()
plt.show()
3. Data voorbewerken
We selecteren de eerste 2 kolommen ('sepal length (cm)' en 'sepal width (cm)') als features: de X-waarden. Als target selecteren we de irissoort.
X = iris.data[:, 2:]
y = iris.target
Vervolgens delen we de data op in 80% train- en 20% testdata. Met de traindata trainen we het model, de testdata gebruiken we om het model te valideren. Hiervoor gebruiken we de methode train_test_split() uit package Scikit-Learn. Het argument stratify=y gebruiken we om in zowel de train- als testdata een gelijke verdeling van irissoorten te krijgen.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42)
4. Algoritme kiezen
Vanuit package Scikit-Learn gebruiken we het algoritme SVC (Support Vector Classifier).
from sklearn.svm import SVC
clf = SVC() #kernel='poly'
clf
SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='scale', kernel='poly',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
5. Model trainen
Met de methode .fit() trainen we het model met de traindata.
clf.fit(X_train, y_train)
SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='scale', kernel='poly',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
6. Model beoordelen
Met de methode .predict() kunnen we nu voor waarden voor 'sepal length (cm)' en 'sepal width (cm)' voorspellingen doen. We doen een voorspelling voor 'sepal length (cm)' = 4cm en 'sepal width (cm)' = 1cm.
clf.predict([[4,1]])
array([1])
iris.target_names[1]
'versicolor'
Dit zou irissoort versicolor moeten zijn. We controleren dit visueel door een grafiek te maken:
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.set(color_codes=True)
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(1,1,1)
for index, target_name in enumerate(iris.target_names):
ax.scatter(X_train[y_train == index, 0], X_train[y_train == index, 1], s=40,
alpha=0.9, edgecolors='k', label=target_name)
ax.plot(4, 1, c='red', alpha=0.9, marker='*', markersize=15);
ax.set_xlabel('petal_length')
ax.set_ylabel('petal_width')
ax.legend()
plt.show()
Dat ziet er goed uit.
Nu bekijken we de nauwkeurigheid (percentage juiste voorspellingen) van het model door dit te bepalen voor voorspellingen op de train- en testdata. Als eerste maken we voorspellingen voor de train- en testdata.
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
Vervolgens gebruiken we accuracy_score() vanuit package Scikit_Learn om de nauwkeurigheid te bepalen.
from sklearn.metrics import accuracy_score
print('Accuracy traindata')
print(accuracy_score(y_train, y_pred_train))
print('')
print('Accuracy testdata')
print(accuracy_score(y_test, y_pred_test))
Accuracy traindata
0.9583333333333334
Accuracy testdata
0.9666666666666667
Ook dit ziet er goed uit. Het model voorspelt op zowel de train- als testdata in meer dan 96% van de gevallen de juiste irissoort. We hebben nu succesvol en SVM model getraind op testdata, en hebben vervolgende hiervan de nauwkeurigheid vergeleken door met het model voorspellingen te doen op train- en testdata.
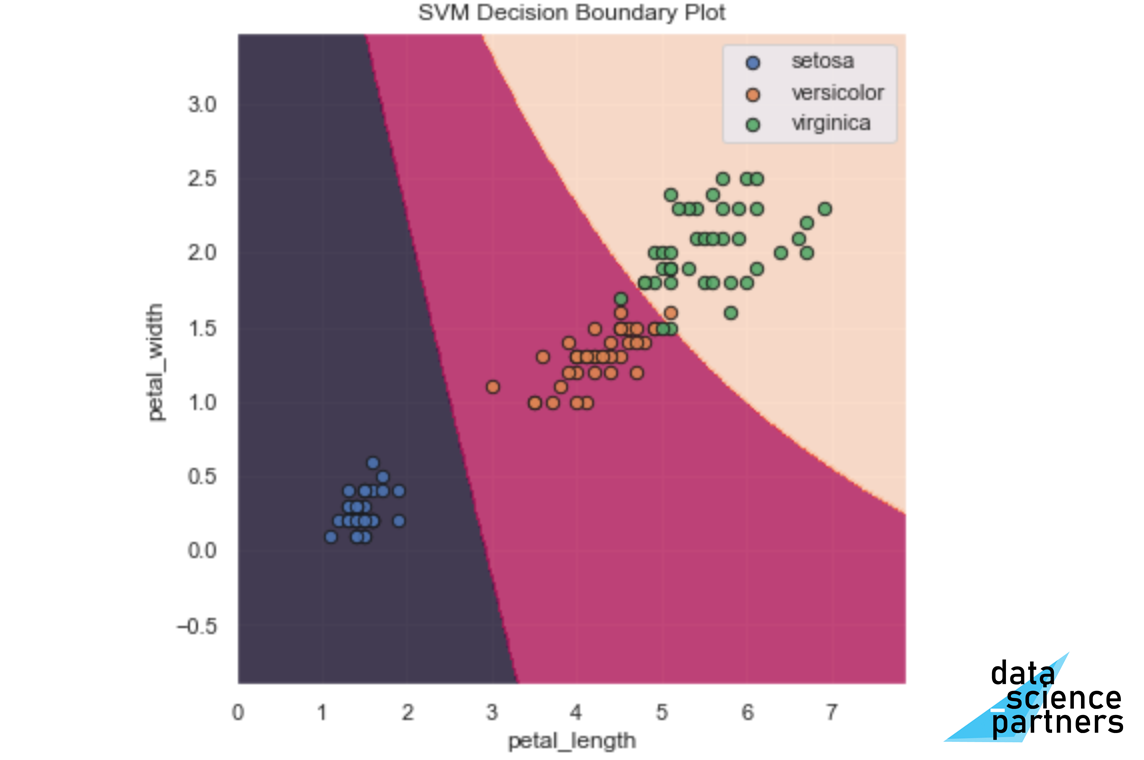
Tot slot kunnen we met een Decision Boundary Plot de grenzen visualiseren van hoe het model met een bepaalde combinatie van input ('sepal length (cm)' en 'sepal width (cm)'), tot een voorspelling komt. Dit doen we met onderstaande code.
import numpy as np
def make_meshgrid(x, y, h=.02):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(1,1,1)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1)
plot_contours(ax, clf, xx, yy, alpha=0.8)
for index, target_name in enumerate(iris.target_names):
ax.scatter(X_train[y_train == index, 0], X_train[y_train == index, 1],
s=40, alpha=0.9, edgecolors='k', label=target_name)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title('SVM Decision Boundary Plot')
ax.set_xlabel('petal_length')
ax.set_ylabel('petal_width')
ax.legend()
plt.show()
Je ziet rechte scheidingslijnen (de hyperplanes). Kijk zelf eens wat er gebeurt als je het model aanpast door de parameter 'kernel='poly'' toe te voegen.
Wat je moet onthouden
Het Support Vector Machine (SVM) algoritme is een Supervised Learning algoritme: er is een beschrijvende dataset nodig om het algoritme toe te passen. SVM maakt gebruik van de best passende scheidingslijnen of vlakken (hyperplanes) om groepen te scheiden. Het SVM algoritme kan zowel gebruikt worden voor classificatie- als regressievraagstukken. SVM is het beste te gebruiken bij kleinere datasets die relatief weinig ruis hebben in de data.
Met Python kun je eenvoudig een SVM algoritme toepassen om een model te maken door gebruik te maken van SVC (classificatie) of SVR (regressie) uit package Scikit-Learn. Hiermee kun je vervolgens met de methode .fit() een model trainen, en met .predict() een voorspelling doen. Nu kun je zelf aan de slag met deze data science toepassing.
Een SVM model stap voor stap toepassen met Python is onderdeel van onze machine learning training en data science opleiding. Dus wil jij je ontwikkelen of omscholen tot data scientist en in staat zijn om nog nauwkeurigere voorspellingen te kunnen doen? Schrijf je dan in of neem contact met ons op voor meer informatie.
Download één van onze opleidingsbrochures voor meer informatie

Peter is een ervaren data scientist en python trainer. Na zijn studie aan de Technische Universiteit Delft heeft hij zich altijd bezig gehouden met data en diverse programmeertalen. Peter heeft veel data analyses uitgevoerd en processen geautomatiseerd met Python in productieomgevingen.